Network Quantization with Element-wise Gradient Scaling

Comparison of straight-through estimator (STE) and element-wise gradient scaling (EWGS). We visualize discrete levels and a loss landscape by straight lines and a contour plot, respectively. In a forward pass, a continuous latent point $\mathbf{x}_n$ is mapped to a discrete point $\mathbf{x}_q$ using a round function. Training a quantized network requires backpropagating a gradient from $\mathbf{x}_q$ to $\mathbf{x}_n$ . (a) The STE propagates the same gradient i.e., $\mathcal{G}_{\mathbf{x}_n}=\mathcal{G}_{\mathbf{x}_q}$ without considering the value of $\mathbf{x}_n$ , where we denote by $\mathcal{G}_{\mathbf{x}_n}$ and $\mathcal{G}_{\mathbf{x}_q}$ the gradients of $\mathbf{x}_n$ and $\mathbf{x}_q$ , respectively. (b) Our approach, on the other hand, scales up or down each element of the gradient during backpropagation, while taking into account discretization errors i.e., $\mathbf{x}_n - \mathbf{x}_q$ .

Authors

Abstract

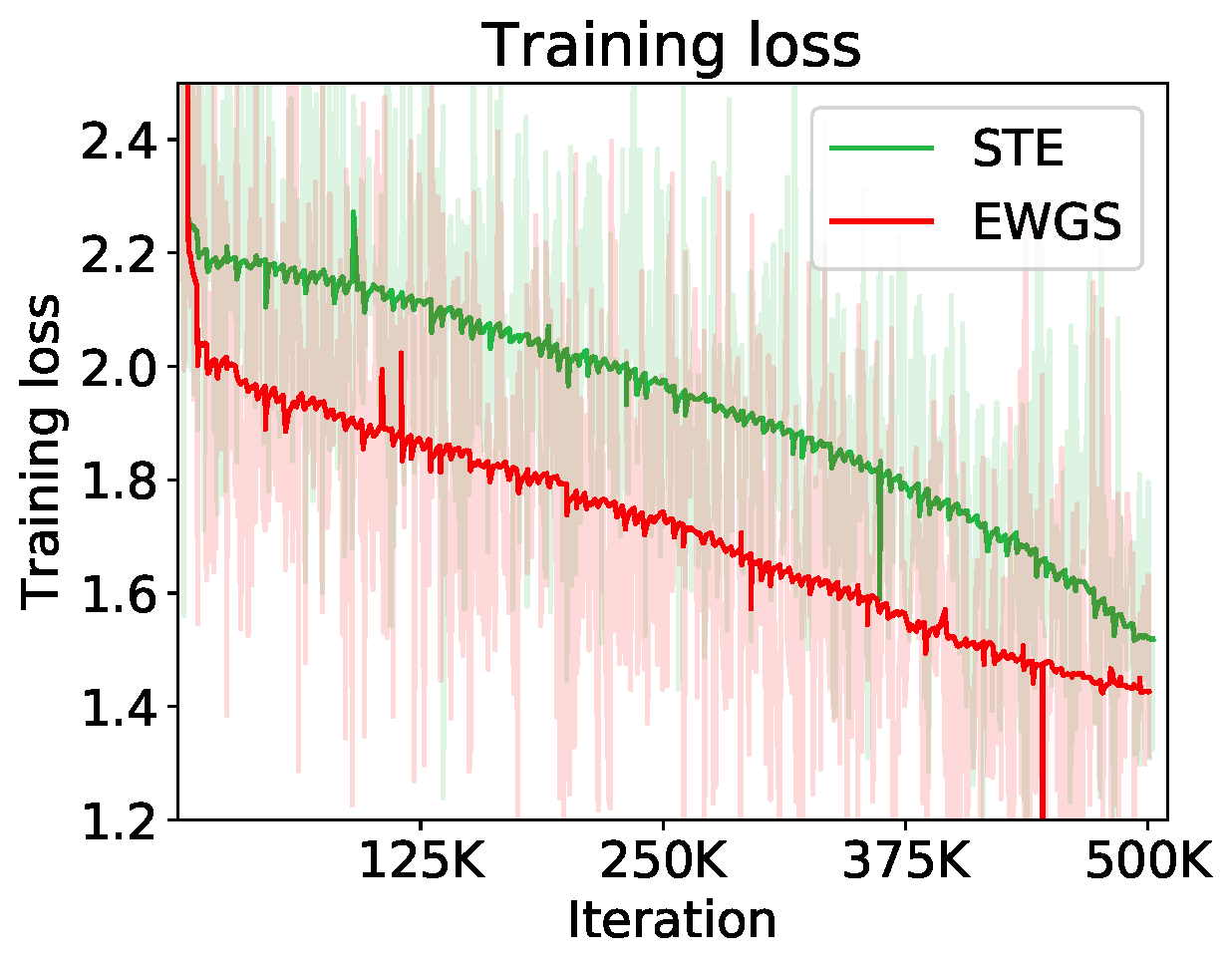
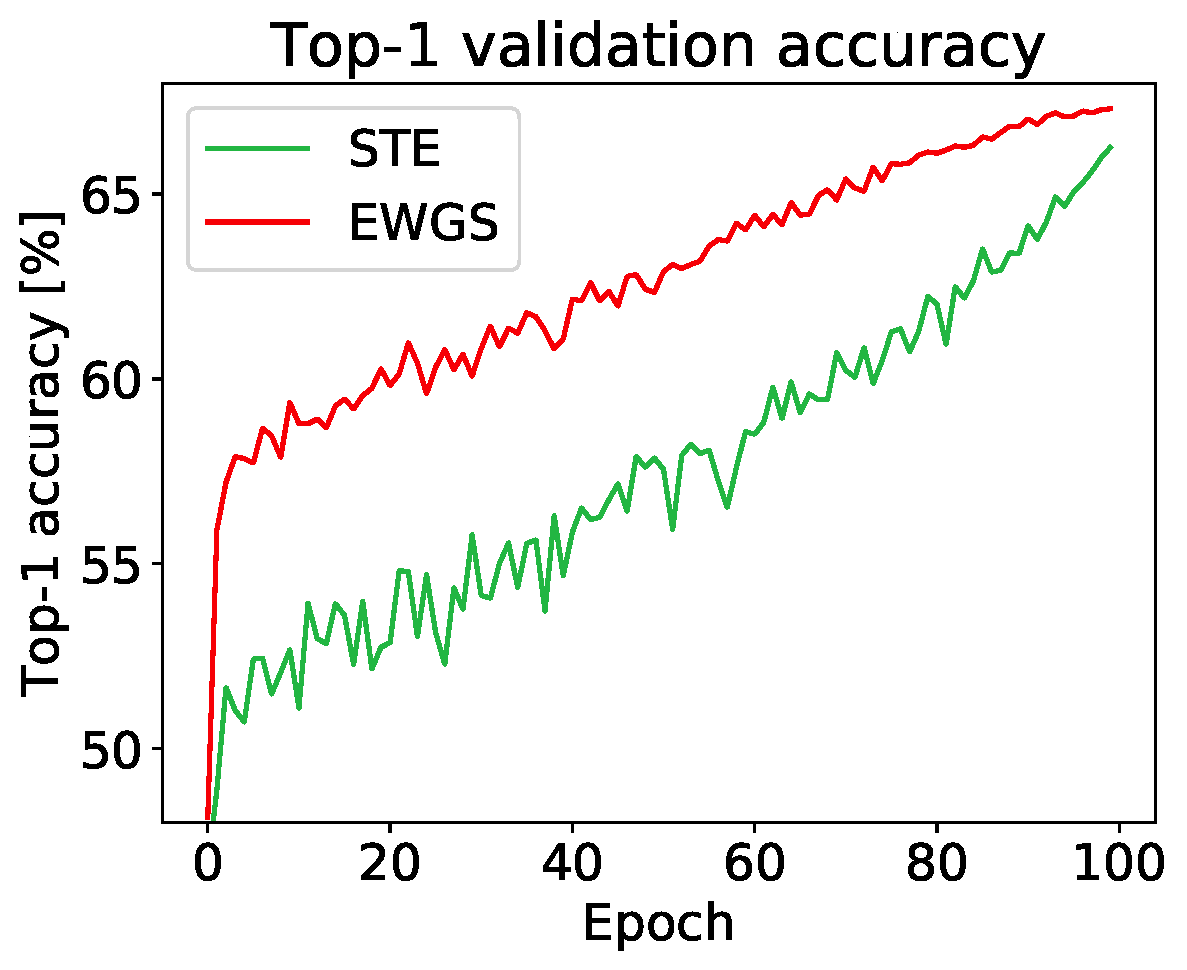
Network quantization aims at reducing bit-widths of weights and/or activations, particularly important for implementing deep neural networks with limited hardware resources. Most methods use the straight-through estimator (STE) to train quantized networks, which avoids a zero-gradient problem by replacing a derivative of a discretizer (i.e., a round function) with that of an identity function. Although quantized networks exploiting the STE have shown decent performance, the STE is sub-optimal in that it simply propagates the same gradient without considering discretization errors between inputs and outputs of the discretizer. In this paper, we propose an element-wise gradient scaling (EWGS), a simple yet effective alternative to the STE, training a quantized network better than the STE in terms of stability and accuracy. Given a gradient of the discretizer output, EWGS adaptively scales up or down each gradient element, and uses the scaled gradient as the one for the discretizer input to train quantized networks via backpropagation. The scaling is performed depending on both the sign of each gradient element and an error between the continuous input and discrete output of the discretizer. We adjust a scaling factor adaptively using Hessian information of a network. We show extensive experimental results on the image classification datasets, including CIFAR-10 and ImageNet, with diverse network architectures under a wide range of bit-width settings, demonstrating the effectiveness of our method.

Method

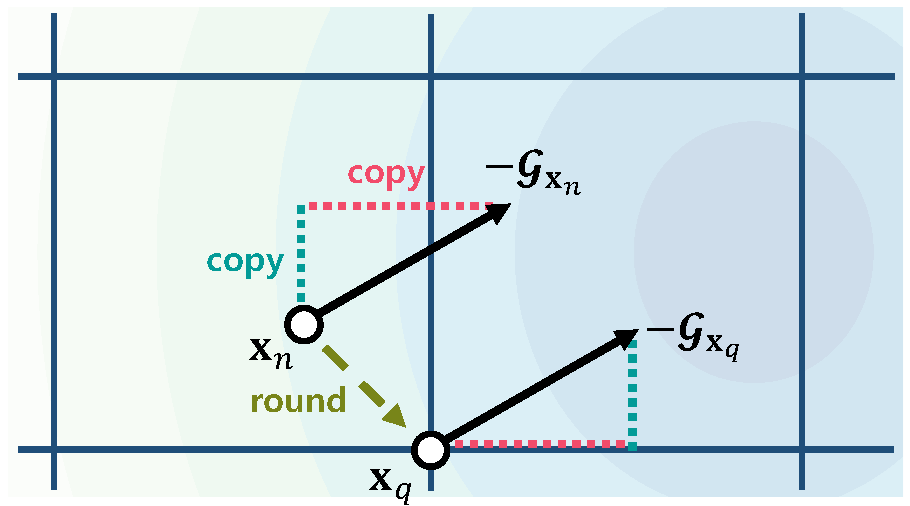
(a) The sign of an update for the discrete value $x_q$ is positive (i.e., $-g_{x_{q}} > 0$ ).

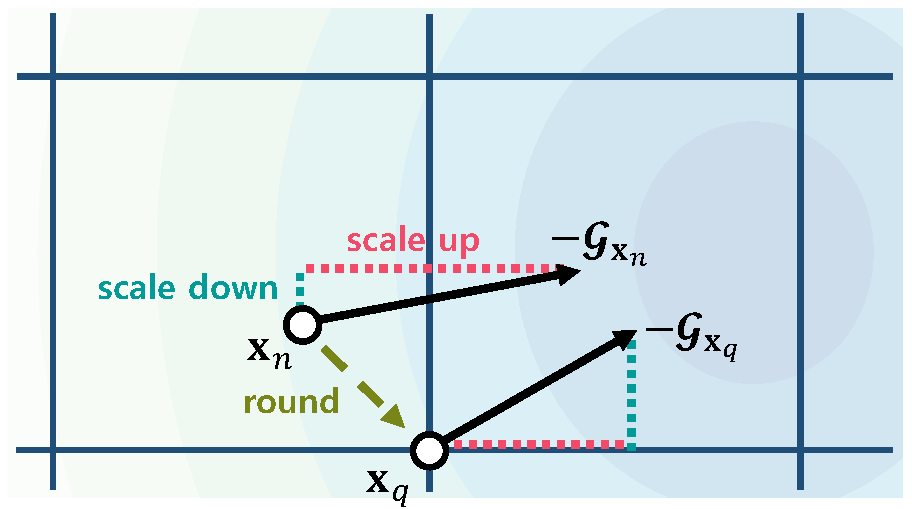
(b) The sign of an update for the discrete value $x_q$ is negative (i.e., $-g_{x_{q}} < 0$ ).

1-D illustrations of EWGS. We visualize a latent value $x_n$ and a discrete value $x_q$ , by red and cyan circles, respectively, where the discrete value is obtained by applying a round function (a dashed arrow) to the latent value. We also visualize their update vectors by solid arrows with corresponding colors, and we denote by $\vert g_{x_n} \vert$ and $\vert g_{x_q} \vert$ the magnitudes of the update vectors for $x_n$ and $x_q$ , respectively. For each (a) and (b), we present three cases, where the latent value $x_n$ is equal to (left), smaller than (middle), and larger than (right) the discrete one $x_q$ . EWGS scales up the gradient element for the discrete value $g_{x_q}$ , when a latent value $x_n$ requires a larger magnitude of an update, compared to the discrete one $x_q$ (e.g., (a)-middle or (b)-right), and scaling down in the opposite case (e.g., (a)-right or (b)-middle). When the latent value $x_n$ is equal to the discrete value $x_q$ , it propagates the same gradient element similar to STE (e.g., (a)-left or (b)-left).

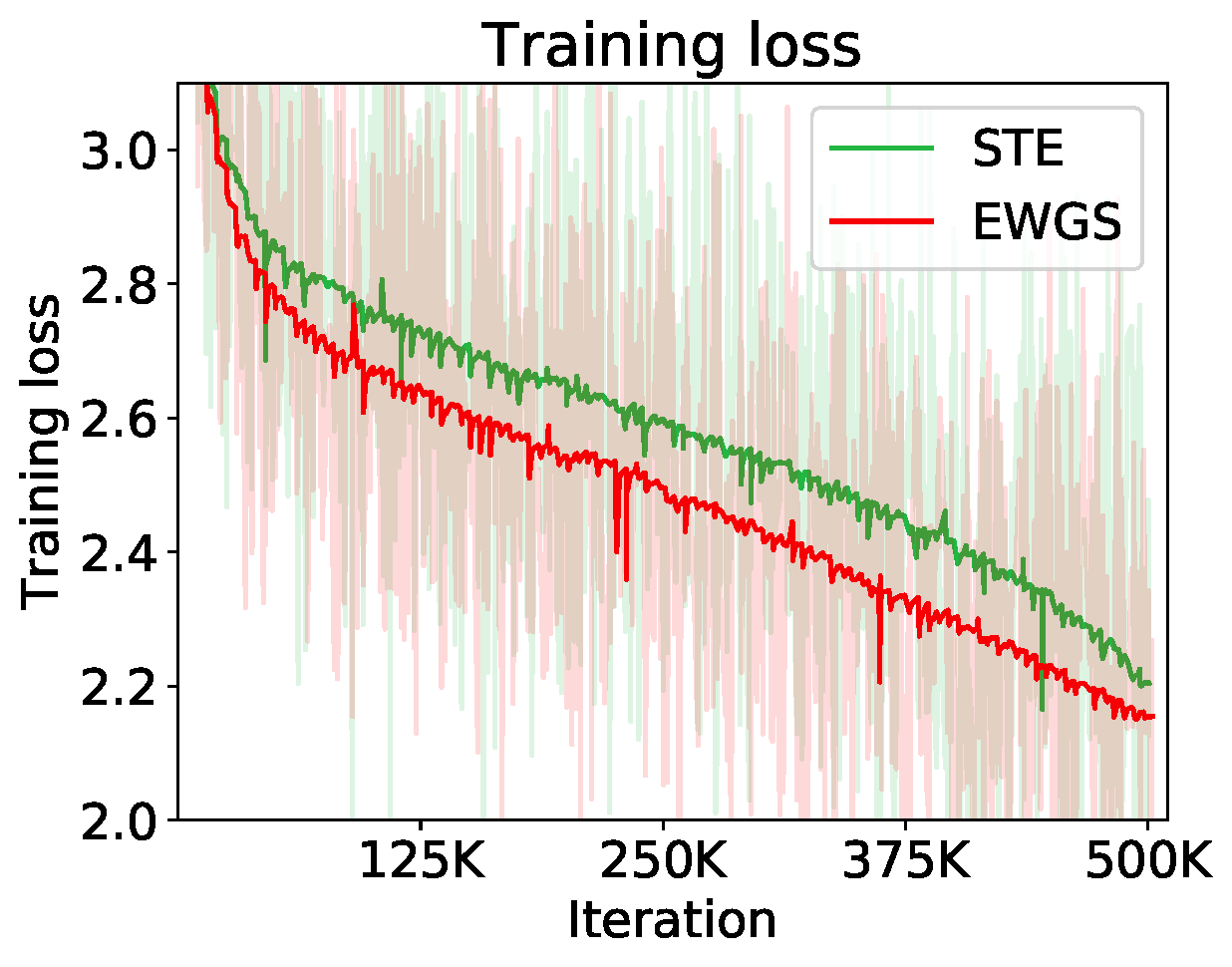
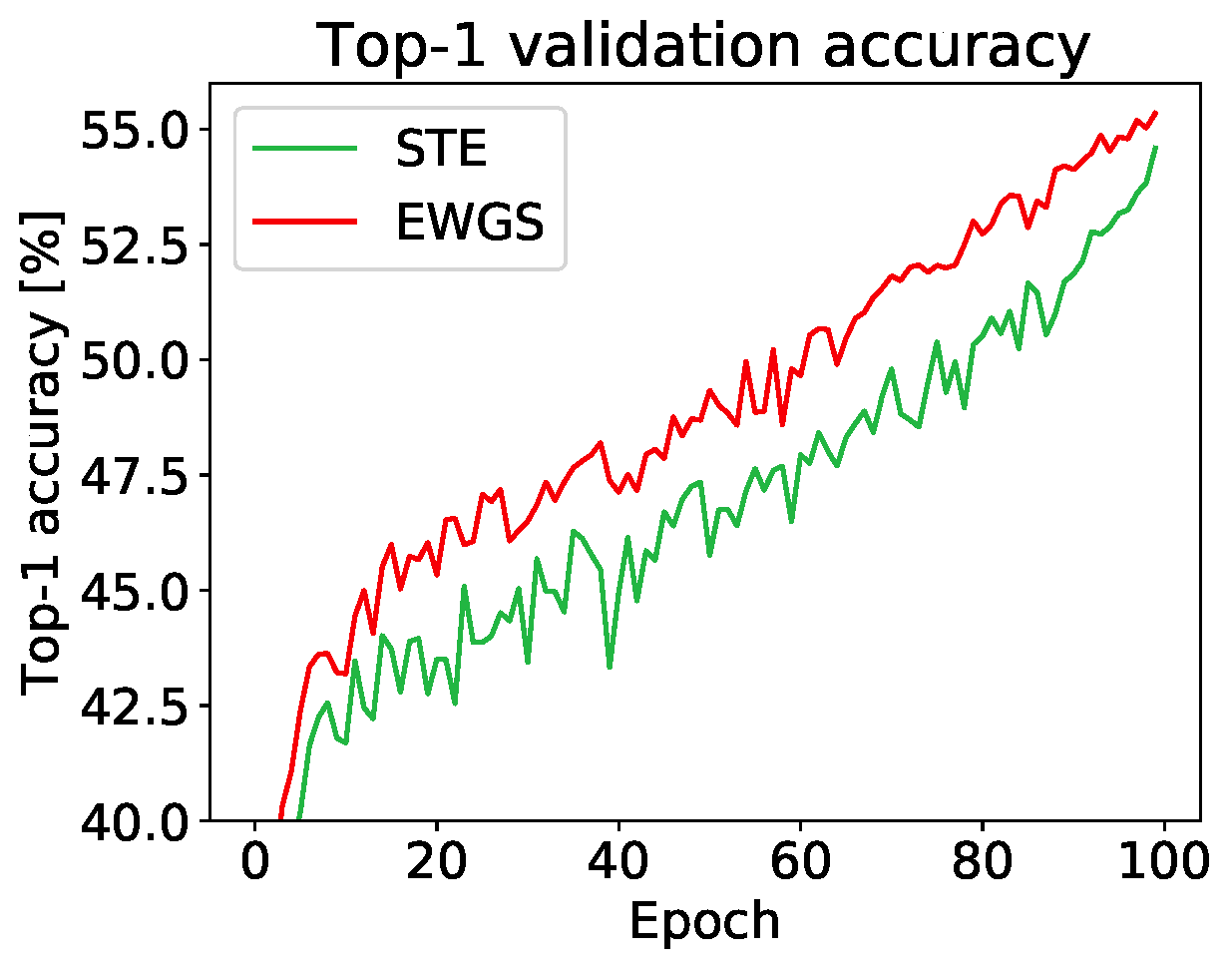
Experiment

Training losses and validation accuracies for binarized networks using STE and EWGS. We use ResNet-18 to quantize (a) both weights and activations and (b) weights only, and show the results on ImageNet.

Paper

J. Lee, D. Kim, B. Ham
Network Quantization with Element-wise Gradient Scaling
In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) , 2021
[Paper on arXiv]

Code

Training/test code (PyTorch)

BibTeX

@inproceedings{lee2021network,
        author       = "J. Lee, D. Kim, B. Ham",
        title        = "Network Quantization with Element-wise Gradient Scaling",
        booktitle    = "Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition",
        year         = "2021"
        }

Acknowledgements

This research was supported by the Samsung Research Funding & Incubation Center for Future Technology (SRFC-IT1802-06).